One hole contexts or:

 how I learned to stop worrying and love the zipper


Me



 
 

What's the Point?



  • Share an interesting data structure
  • Show some Scala code

Remind you to ignore math
at your peril!

What is a Zipper?



  • Reification of a walk
  • Derivative of a data structure
  • A data structure with a hole
  • Just something useful

Something Useful


It allows us to navigate a data structure and modify components as we go along

"Solving" the in-place edit "problem"

Something Useful



  • O(1) - In Place Update


vs

  • O(n)/O(log n) - Update

Something Useful


Take a List[T],

we can make a Zipper of form,

(before: List[T], focus: T, after: List[T])

Example 1


val ls = List('a','b','c','d','e')

if 'd' is the focus

val zipper = (['c','b','a'],'d',['e'])

Zipped List


case class ZippedList[T](before: List[T], focus: T,
                         after: List[T]) {
  def goLeft(): ZippedList[T] = before match {
    case Nil => throw new Exception("Can't move left")
    case x::xs => ZippedList(xs,x,focus::after)
  }
  def goRight(): ZippedList[T] = after match {
    case Nil => throw new Exception("Can't move right")
    case x::xs => ZippedList(focus::before,x,xs)
  }
  def update(f: T => T): ZippedList[T] =
    ZippedList(before,f(focus),after)
  def zipUp(): List[T] = (focus :: before).reverse ++ after
}

Form




PATH, FOCUS, REST

Trees


Take a binary tree with values,

abstract class BTree[A]
case class Leaf[A](value: A) extends BTree[A]
case class Node[A](value: A, left: BTree[A],
                   right: BTree[A]) extends BTree[A]

Zipper


Simplify to Path, Focus


case class ZippedTree[T](path: List[Decision[BTree[T]]],
                         focus: BTree[T])

Go Left


def goLeft() : ZippedTree[T] = focus match {
  case Leaf(_) => throw new Exception("Can't move left") 
  case Node(_,l,_) => ZippedTree(Left(focus)::path,l)
}

Defs


abstract class Decision[T]
case class Left[T](value: T) extends Decision[T]
case class Right[T](value: T) extends Decision[T]

Go Right


def goRight() : ZippedTree[T] = focus match {
  case Leaf(_) => throw new Exception("Can't move right")
  case Node(_,_,r) => ZippedTree(Right(focus)::path,r)
}

Go Up


def goUp() : ZippedTree[T] = path match {
  case Nil => throw new Exception("Can't go up")
  case Left(Node(v,_,r)) :: rest =>
    	ZippedTree(rest,Node(v,focus,r))
  case Right(Node(v,l,_)) :: rest =>
    	ZippedTree(rest,Node(v,l,focus))
}

Update


def update(f: BTree[T] => BTree[T]): ZippedTree[T] =
  ZippedTree(path,f(focus))

ZipUP


def zipUp(): BTree[T] = {
  def rollup(z: ZippedTree[T]): BTree[T] = z match {
    case ZippedTree(Nil,f) => f
    case x => rollup(x.goUp())
  }
  rollup(this)
}

Example


val t: BTree[Int] = Node(1,
		         Node(7,
		              Leaf(3),
			      Leaf(4)),
			 Node(7,
			      Node(7,
				   Leaf(9),
				   Leaf(2)),
			 Leaf(4)))

Example...


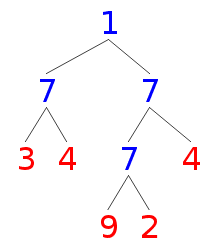
syntax

Live code...


<Insert bad demo here...>

What else can we Zip?


  • N-ary Trees
  • Streams
  • ...any simple sum, product or recursive type

Maths interlude...


What are we doing?

Really all about creating paths to the current focus

Maths interlude...


Bit more formality

Path is a list of decisions, so let's annotate our decision and store the siblings of a node in the tree.

Maths interlude...


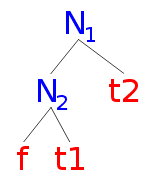
syntax

path to f is;

Left(N2) :: Left(N1)

Maths interlude...


Left(N2) :: Left(N1) + f => ZIPPER

Since we can recover the tree from the Zipper,

Left(N2) :: Left(N1) is the tree minus f,

the tree with a hole

One hole contexts


Left(N2) :: Left(N1)

That's a one hole context of BTree,

where BTree is a product type of Leaf | BTree*BTree

The notation * indicates a product type.
Think any tree with any other tree

You can do the same for ternary trees
Leaf | TTree*TTree*TTree

One hole contexts...


Each decision we make in a BTree has the type

Decision[Btree] which can be expressed
Left(BTree) | Right(BTree)

Which happens to be a sum type, BTree+BTree

Think all lefts and all rights

One hole contexts...


So a generous rewriting may give us,

BTree = 1 + BTree^2

TTree = 1 + TTree^3

∂BTree = 2BTree

∂TTree = 3TTree …

One hole contexts...


The derivative of a regular type is its type of one-hole contexts

So...?


In theory it is possible to synthesise a Zipper from any regular type, with arbitrary navigation and update.

So...?


In practise we need more type-level programing...

Questions?


... Easy ones only!

References